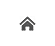2018年1月17日~19日にかけて、Maxim D. Ballmer博士 (チューリッヒ工科大学)による集中講義を東京大学にて開催いたしました。東京大学の学部生及び大学院生を含む5名が出席し、マントル対流の数値計算についての講義や数値計算演習に取り組みました。
<学生の声>
この集中講義は私にとって、マントル対流計算のモチベーションや手法を詳しく学ぶ初めての機会でした。講義ではマントル対流計算の地球科学における位置付けや研究成果を分かりやすく(対流の様子を表す美しい図が印象的でした)解説していただきました。後半の演習ではサンプルのMatlabコードを提供していただき、手を動かしながらマントル対流の数値計算を体験することができました。自身の研究分野とも関わりが強いため、これまでにもマントル対流計算の研究論文を読んだり研究発表を聞いたりしたことはありましたが、この講義で実際の数値計算がどのように行われているかを経験することができました。今後の研究活動に活かしていきたいと考えています。さらにこの集中講義には、地球科学の学生だけでなく惑星科学・天文学の参加学生と交流を持つことができた良い機会でした。 (D1 鈴木裕輝)
The lecture of Dr. Maxim D. Ballmer gave me a much better understanding of how the models of mantle convection are built. Seismologists imaging the structure of the mantle using seismic tomography rely heavily on models of mantle convection, e.g. to understand what happens to slabs when they penetrate in the lower mantle, or the formation of plumes from large thermochemical piles at the bottom of the Earth’s mantle. The simulations of thermochemical convection that we ran during the practical session of the course gave me a good idea of how important physical parameters (e.g. diffusivity, thermal expansion, density) affect convection, which will really help me to understand more precisely the work of geodynamicists. (Anselme Borgeaud, PhD student in Seismology)
| 日時 | 2018年1月17日(水)~19日(金)の三日間 17日:2~4限 18日:2~3限 19日:2~4限 2 時限 10 時 25 分 ~ 12 時 10 分 3 時限 13 時 00 分 ~ 14 時 45 分 4 時限 14 時 55 分 ~ 16 時 40 分 |
| 場所 | 東京大学 理学部1号館8階839号室ほか(変更になる可能性があります) |
| 講師 | Maxim D. Ballmer博士(ETH Zürich) |
| 講義題目 | 固体地球科学特論II |
| 講義の目標・概要 | This course will provide the theoretical background of mantle convection on terrestrial planets, teach the basics of numerical modeling of fluid dynamics with solid-Earth applications, and also give examples of how to test numerical-model predictions with geological, geochemical, and geophysical observations. The goal of this course is to understand the objectives and potentials of numerical modeling, as well as to learn how to program a simple isoviscous thermo-mechanical model using finite-difference discretization. Basic knowledge of a programming language is desired but not necessarily required. |
| 講義スケジュール |
1. Background on Mantle Convection 2. Comparing model predictions with observation at the example of geodynamic simulations of the mantle plume 3. Thermochemical convection and numerical-model predictions 4. Introduction of the finite difference approximation for the solution of differential equations. Introduction to programming in Matlab 5. Solving the 1D and 2D Poisson equation 6. Solving the momentum and continuity equations 7. Boundary conditions (free-sip, no-slip) and solving the heat equation 8. Developing a coupled thermo-mechanical model for isoviscous mantle convection |
| 問い合わせ | A03-1 河合研志(kenji-at-eps.s.u-tokyo.ac.jp) |